Introdução
Em um artigo anterior, tratei do problema da construção de estruturas de dados genéricas, isto é, estruturas capazes de manipular diferentes tipos de dados, informados no momento da criação destas estruturas. No final deste artigo, levantei a seguinte questão:
Como podemos criar uma função comparar os itens de uma estrutura de dados genérica, uma vez que ela não conhece o seu tipo, a priori. Mesmo sabendo qual é o tipo de dado, em alguns casos, não seria possível compará-los; por exemplo, quando o tipo de dado é uma estrutura complexa, criada pelo próprio desenvolvedor, como uma struct para armazenar os dados de um aluno, entre outros.
Para resolver este problema, utilizando a linguagem C, precisamos lançar mão de um recurso conhecido como funções callback. Esse tipo de função tira proveito do fato de que a linguagem C trabalha com ponteiros para funções, isto é, podemos passar para uma função, um ponteiro que aponta para o bloco da memória onde está localizada outra função do sistema (ou até mesmo a própria função que está recebendo o parâmetro). Isto permite que uma determinada função chame outras funções, mesmo sem ter conhecimentos de quais funções são estas.
Neste artigo, pretendo trabalhar com a questão das funções callback, envolvendo um assunto bastante explorado nas disciplinas de algoritmos e estruturas de dados, a saber, a ordenação. Ordenar é o processo de rearranjar um conjunto de objetos em uma ordem ascendente ou descendente. A ordenação visa a facilitar a recuperação posterior de itens do conjunto ordenado. Imagine, por exemplo, utilizar um catálogo telefônico, no qual os nomes das pessoas não estão organizados em ordem alfabética. Ou então utilizar um dicionário, no qual as palavras não estão listadas em ordem alfabética.
A maioria dos métodos de ordenação é baseada em comparação de chaves. Qualquer tipo de chave sobre o qual exista uma regra de comparação bem definida pode ser utilizado. De modo análogo ao que foi comentado no nosso artigo anterior, quando cursamos disciplinas de Algoritmos e Estruturas de Dados nos cursos de computação e áreas afins, em geral, aprendemos a implementar algoritmos de ordenação capazes de trabalharem apenas com números inteiros. Isto não é essencialmente um problema, uma vez que o intuito destas disciplinas é apresentar os principais tipos de algoritmos, suas aplicações e complexidades de tempo e espaço.
Contudo, quando vamos para a prática do desenvolvimento, ao utilizarmos estes algoritmos, sejam em um trabalho prático da disciplina ou em outro tipo de situação, nosso desejo será trabalhar com implementações capazes de ordenar qualquer tipo de elemento e não apenas de números inteiros.
Neste sentido, este artigo tem como objetivo apresentar o desenvolvimento de um algoritmo de ordenação simples, o Selection Sort (ordenação por seleção) de forma genérica, isto é, de forma que ela seja capaz de ordenar qualquer tipo de elemento especificado pelo usuário, sem exigir que seu código seja modificado.
O algoritmo de ordenação Selection Sort
Selection Sort (ou ordenação por seleção) é um dos algoritmos de ordenação mais simples. O pseudocódigo desse algoritmo pode ser descrito da seguinte forma:
- Selecione o menor elemento do vetor;
- Troque-o com o elemento da posição do início do vetor (após isto a posição de início apontará para a próxima posição do vetor);
- Repita essas duas operações com os n – 1 elementos restantes, depois com os n – 2 elementos, até que reste apenas um elemento.
A Figura 1 ilustra o funcionamento do método de ordenação Selection Sort, segundo descrito anteriormente.
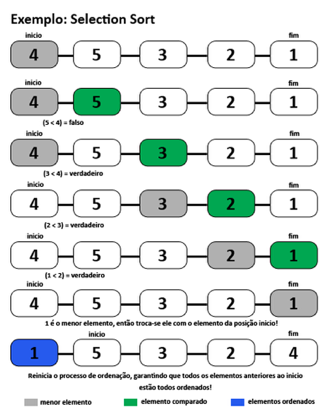
Analogamente, sua implementação na linguagem de programação C é bastante simples, conforme é apresentado na seguinte listagem.
void ordenacaoPorSelecao(int vetor[], int n) {
for(int i = 0; i < n - 1; i++) {
int menor = i;
for(int j = i + 1; j < n; j++) {
if (vetor[j] < vetor[menor]) menor = j;
}
int aux = vetor[i];
vetor[i] = vetor[menor];
vetor[menor] = aux;
}
}O comando for mais interno deste algoritmo, linhas 4 à 6, é responsável por encontrar o menor elemento do vetor, cujos índices vão de i + 1 a n – 1. As linhas 7 à 9 são responsáveis por colocar o menor elemento identificado pelo for mais interno em sua posição correta. O comando for mais externo é responsável por percorrer todo o vetor, permitindo que todos os elementos sejam colocados no lugar certo. O valor da variável i deste comando representa a posição atual onde o menor elemento deverá ser colocado.
A análise da complexidade deste algoritmo, em função do número de comparações realizadas pelo mesmo, também é bem simples. Imagine um vetor de N elementos. Na primeira execução, o comando if será executado N – 1 vezes. Na segunda, N – 2. Na terceira, N – 3 e, assim sucessivamente, até a N-ésima – 1 vez, na qual o comando if será executado apenas 1 vez. Portanto, o número de comparações, C(n), realizada por este algoritmo é dado por:
C(n) = 1 + 2 + 3 + … + N-1
C(n) = [(N-1) * (N – 1 + 1)]/2
C(n) = (N2 – N)/2
Resumindo, em termos do número de comparações, este algoritmo é da classe quadrática, O(n2), de complexidade de tempo. Quanto ao número de movimentações realizadas pelo algoritmo, a análise é mais simples ainda. Ao executar o algoritmo passo a passo é possível observar que ele sempre irá realizar N – 1 movimentações para um vetor de tamanho N. Ou seja, em termos da quantidade de movimentações realizadas pelo algoritmo, Selection Sort é da classe de complexidade linear: O(n). Este é um resultado interessante para o número de movimentações, se comparado a outros algoritmos de ordenação, como o Bubble Sort ou o Insertion Sort, em seus piores casos.
Outra característica interessante deste algoritmo de ordenação é que o mesmo apresenta a mesma complexidade, qualquer que seja a configuração do vetor de entrada. Isto é, dado um vetor de tamanho N, não importa se o vetor está parcialmente ou totalmente ordenado, ou se está ordenado inversamente, a quantidade de comparações e movimentações a serem realizadas será sempre a mesma. Diferentemente de outros métodos de ordenação, que são sensíveis à configuração da entrada, como por exemplo o Insertion Sort, que apresenta um número de comparações bem menor quanto o vetor está totalmente ou parcialmente ordenado.
Outro ponto que chama a atenção no código da listagem anterior é que a função ordenacaoPorSelecao recebe como parâmetro um vetor de números inteiros e um inteiro que representa o tamanho deste vetor. O fato de ela receber um vetor de inteiros em sua definição, a impede de trabalhar com conjuntos referentes a outros tipos de dados, como strings ou até mesmo tipos complexos, como registros de “Alunos”, “Notas”, “Processos”, entre outros.
A questão chave é: o algoritmo de ordenação tem como responsabilidade colocar em ordem crescente ou decrescente um conjunto de registros, cujas chaves possam ser comparadas de alguma maneira. A priori, não é responsabilidade do algoritmo de ordenação saber como comparar dois registros de um conjunto de dados. Isso está relacionado ao domínio do problema que está sendo resolvido com o algoritmo de ordenação. Neste sentido, vamos aprender a criar um algoritmo de ordenação genérico, isto é, que seja capaz de ordenar qualquer conjunto de dados, sem se preocupar com o tipo destes dados.
Selection Sort Genérico
Antes de implementarmos o Selection Sort genérico, faz-se necessário conhecer o recurso da linguagem C que utilizaremos para atingir nosso objetivo. Este recurso se chama função callback, que pode ser implementado por meio do uso de ponteiros para função.
Muitos devem conhecer o uso de ponteiros em C para alocação dinâmica de memória, bem como para passagem de parâmetros por referência para funções. Além dessas possibilidades oferecidas pelos ponteiros, é possível também definirmos ponteiros para funções dentro do nosso programa. Assim, teremos uma variável que aponta para uma região de memória onde não estão alocados dados, mas sim instruções de alguma função pré-definida no programa.
Isto permite que direcionemos o fluxo de execução de nosso programa para outro ponto, sem a necessidade de sabermos, a priori, para onde estaremos indo. Dá para perceber que este é um recurso que deve ser usado com parcimônia, para que não transformemos o código do nosso programa em um código “macarrônico”, isto é, que seja “impossível” de se acompanhar o que está acontecendo durante a execução do programa.
O uso de ponteiros para funções é interessante quando desejamos executar alguma rotina e que partes dessa rotina sejam definidas por outras funções, cuja definição seja passada por parâmetro (funções callback).
A seguinte listagem apresenta um exemplo da utilização de ponteiros para funções e de uma função callback. O código fonte da função ordenacaoPorSelecao foi omitido, uma vez que é idêntico ao apresentado anteriormente.
#include <stdio.h>
#include <stdlib.h>
void ordenacaoPorSelecao(int vetor[], int n) { ... }
void imprimirVetor(int vet[], int n) {
printf("[");
for(int i = 0; i < n - 1; i++) {
printf("%d ", vet[i]);
}
printf("%d]\n", vet[n - 1]);
}
void ordenacao(int vet[], int n, void (*funcOrd)(int[],int)) {
printf("Vetor original: "); imprimirVetor(vet, n);
funcOrd(vet, n);
printf("Vetor ordenado: "); imprimirVetor(vet, n);
}
int main() {
int vet[5] = {4, 5, 3, 2, 1};
ordenacao(vet, 5, &ordenacaoPorSelecao);
return EXIT_SUCCESS;
}Este programa declara um vetor de cinco elementos aleatórios, linha 18 e invoca a função ordenacao, que é responsável por imprimir o vetor em sua forma original, ordená-lo e depois imprimir novamente o vetor, só que agora ordenado. A saída da execução do programa acima é a seguinte:
Vetor original: [4 5 3 2 1]
Vetor ordenado: [1 2 3 4 5]
O interessante, e talvez novo para você, leitor, está nas linhas 12, 14 e 19. A linha 12 apresenta a declaração do parâmetro void (*funcOrd)(int[],int): este parâmetro é um ponteiro para uma função do programa. Esta função tem as seguintes características: seu tipo de retorno é void, seu identificador (que será utilizado para invocá-la dentro da função ordenacao) é funcOrd e ela recebe dois parâmetros, um vetor de inteiros e um inteiro.
Neste ponto, estamos declarando uma função callback, ou seja, uma função que será invocada a partir de um ponteiro, cujo valor será informado pelo usuário no momento da invocação da função ordenacao.
Veja que a função ordenacao invoca funcOrd na linha 14, passando os parâmetros exigidos por ela, porém ordenacao não tem conhecimento sobre qual função está sendo executada neste momento. Isto que dizer que para a função ordenacao não importa saber qual algoritmo de ordenação está sendo utilizado para organizar os elementos do vetor, mas sim, que eles estarão ordenados após o término da execução desta função.
A última linha a ser analisada é a 19; nesta linha está a chamada para a função ordenacao, passando como parâmetro o endereço de memória onde encontra-se alocada a função ordenacaoPorSelecao. Para obter o endereço de memória de variáveis e funções, o operador & é utilizado antes do identificador deste elemento.
O maior benefício está em podermos substituir facilmente o método de ordenação utilizado na função ordenacao. Para fazer isso, bastaria implementar uma nova função de ordenação e passar o endereço dela como parâmetro para a função ordenacao.
Com este exemplo, creio ter ficado fácil imaginar como será implementado o método de ordenação Selection Sort genérico. Como dissemos anteriormente, o método não deve se preocupar em como os registros são comparados, pois isso depende do que o usuário está querendo ordenar. Sendo assim, nossa função callback será uma função capaz de comparar dois registros quaisquer e dizer se eles são iguais ou qual registro é maior do que o outro.
A listagem seguinte apresenta a implementação do algoritmo de ordenação Selection Sort genérico, bem como a utilização do mesmo para ordenar um conjunto de números inteiros.
#include <stdio.h>
#include <stdlib.h>
#define MENOR -1
#define IGUAL 0
#define MAIOR -1
int compararInteiros(void* n1, void* n2) {
int a = *((int*)n1); int b = *((int*)n2);
if (a < b) return MENOR;
else if (a > b) return MAIOR;
else return IGUAL;
}
void ordenacaoPorSelecao(void* vetor[], int n, int (*comp)(void*,void*)) {
for(int i = 0; i < n - 1; i++) {
int menor = i;
for(int j = i + 1; j < n; j++) {
if (comp(vetor[j], vetor[menor]) == MENOR) menor = j;
}
void* aux = vetor[i];
vetor[i] = vetor[menor];
vetor[menor] = aux;
}
}
void imprimirVetor(void* vet[], int n) {...}
int main() {
int a = 4, b = 3, c = 1;
int* vet[3] = {&a, &b, &c};
printf("Vetor original: "); imprimirVetor(vet, 3);
ordenacaoPorSelecao(vet, 3, &compararInteiros);
printf("Vetor ordenado: "); imprimirVetor(vet, 3);
return EXIT_SUCCESS;
}Os trechos de código importantes a serem observados na listagem são:
- Linhas 7 à 11: a função
compararInteirosserá passada como parâmetro para a funçãoordenacaoPorSelecao, isto é,compararInteirosé a função callback responsável por comparar dois registros, que neste caso, são números inteiros. Esta função recebe dois ponteiros do tipovoid, os converte em ponteiro para inteiros para assim poder compará-los. Caso o usuário quisesse comparar outros tipos de dados, bastaria implementar uma função capaz de comparar dois registros do tipo desejado; - Linhas 13 à 23: a função
ordenacaoPorSelecaofoi alterada de modo que, agora, ela não trabalha mais com base em um tipo específico de dados, mas sim com registros do tipovoid, isto é, tipos genéricos. Além disso, outra modificação significativa é que esta função passa a receber um parâmetro a mais, que é o endereço de memória de uma função capaz de comparar dois registros do conjunto de dados passado para a funçãoordenacaoPorSelecao. Está função é declarada comocompna assinatura da funçãoordenacaoPorSelecaoe é invocada na linha 17, no momento em que dois elementos do conjunto de dados precisam ser comparados; e - Linhas 25 à 32: por fim, a função
mainsofreu algumas pequenas mudanças para comportar a nova implementação da funçãoordenacaoPorSelecao. Por exemplo, ao invocar a funçãoordenacaoPorSelecao, o endereço da funçãocomparaInteirosprecisou ser passado como parâmetro.
Considerações Finais
Em uma olhada rápida no código da última listagem, pode-se julgar que os benefícios da mudança realizada não compensaram o esforço necessário para realizá-la. Contudo, pode-se perceber que a partir deste momento, o algoritmo de ordenação por seleção está preparado para lidar com qualquer tipo de dados, desde que seja oferecida a ele uma função adequada para comparação de elementos do tipo desejado. Isto evitará duplicação de código e facilitará a implementação de programas que trabalham com conjuntos de dados de diversos tipos, garantindo maior flexibilidade ao programa como um todo, além de não ter necessidade de reescrever as mesmas rotinas para se adaptarem as implementações que suportem novos tipos de dados, dando maior flexibilidade ao desenvolvedor.
É válido ressaltar que esta técnica se aplica a linguagens de programação que suportem somente o paradigma estruturado, como por exemplo a linguagem C, que foi a linguagem utilizada neste artigo. Em linguagens de programação mais recentes que suportem o paradigma de orientação a objetos (Java, C++, Python), devido a sua essência, este paradigma nos fornece maior suporte para desenvolver métodos mais eficientes para realizarmos a ordenação genérica abordada neste artigo.
Com o conhecimento adquirido neste artigo, fica como exercício a implementação de outros algoritmos de ordenação de forma genérica.